
맥스웰 방정식은 다음과 같이 총 4가지가 있다. 이제 이에 대해 공부해보려고 한다.
(1) 전기에 대한 Gauss의 법칙

그림 23-1은 가상적인 구에 둘러싸여 있는 전하 Q인 입자를 나타낸다. (Gauss 표면이라고 불림) 구 위의 점에서 전기장 벡터는 적당한 크기를 갖고 입자로부터 지름방향으로 멀어지는 방향으로 향한다. 전기장선 또한 바깥 방향이고, 적당한 밀도를 가지고 있다. 이 때 전기장 벡터와 전기장선은 표면을 뚫고 지나간다고 한다.

그림 23-2는 비슷한 그림이지만 둘러싸인 입자의 전하가 +2Q이다. 둘러싸인 전하가 두 배 커졌으므로, Gauss 표면을 바깥 방향으로 뚫고 지나가는 전기장 벡터의 크기도 그림 23-1보다 두 배 커졌고, 또한 전기장선의 밀도도 두 배가 된다.
이 표현이 간단히 말하면 Gauss 법칙이다.
=> Gauss 법칙은 (닫힌) Gauss 표면 위의 점에서 전기장과 이 표면으로 둘러싸인 전하 사이의 관계를 맺는다.
*전기다발

우선 균일한 전기장 벡터 E 안에 있는 면적 A인 평편한 표면부터 시작하자. 그림 (a)에 면적 델타A인 작은 작은 정사각형 조각을 지나가는 전기장선 중의 하나를 나타내었다.
조각을 지나가는 전기장의 크기는 이것을 지나가는 전기다발로 정의한다.

알짜다발의 경우 다음과 같다.

여기서 Gauss 법칙은 폐곡면(Gauss면)을 통과하는 전기장의 알짜다발과 Gauss면으로 둘러싸인 알짜 전하 사이의 관계를 나타내는 식으로 다음과 같다.
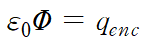
전기장 다발을 정의한 식을 위 식에 대입하여 정리하면

(2) 자기에 대한 Gauss의 법칙

위 그림은 막대 자석 위에 투명판을 놓고 그 위에 뿌려놓은 쇳가루의 모양이다. 쇳가루 알갱이들은 자석의 전기장을 k라 정렬하기 때문에, 쇳가루들은 자기장을 나타내는 무늬를 따라 배열한다. 자석의 한 끝은 자기장의 발생원(자기장선이 여기로부터 퍼져나간다)이고, 다른 끝은 수렴원(자기장선이 여기로 모여든다)이다. 편의상 발생원은 자석의 북극이라 하고, 수렴원은 남극이라고 부른다. 이와 같이 두 극을 가지고 있는 자석은 자기쌍극자의 일종이다.

막대자석을 분필처럼 여러 조각으로 부러뜨렸다고 생각해보자.(위 그림 참고) 그러면 자기홀극이라고 부를 수 있는 하나의 자기극을 분리할 수 있을까? 사실은 분리할 수 없다. 자석을 개별 원자로 갈라놓는 정도가 아니라 전자와 핵으로 분리해도 안 된다. 모든 조각이 북극과 남극을 가지고 있기 때문이다. 따라서 다음과 같이 말할 수 있다.
가장 간단한 자기적 구조는 자기쌍극자이다. 자기홀극은 (우리가 알고 있는 한) 존재하지 않는다.
자기장에 대한 Gauss의 법칙은 자기홀극이 존재하지 않는다는 말을 수식화한 것이다. 즉, 다음 식처럼 폐곡면(Gauss면)을 통과하는 알짜 자기다발은 0이다.

(3) Faraday의 법칙
간단하게 말해 자기장과 전기장 사이의 유도관계를 Faraday의 법칙이라고 한다. 일단 먼저 2가지 실험을 보자.
첫 번째 실험

그림을 보면 민감한 전류계에 연결된 도체 고리가 있다. 이 회로에는 전지나 다른 기전력장치가 없기 때문에 전류가 흐르지 않는다. 그러나 막대자석을 전류고리 쪽으로 움직이면 회로에 갑자기 전류가 흐르다가 자석의 움직임이 멈추면 사라진다. 한편 자석이 전류고리에서 멀어지면 다시 전류가 흐르게 되는데, 이 때 전류는 반대 방향으로 흐른다. 이 실험을 통해 다음과 같은 사실을 알 수 있다.
전류고리와 자석 사이에 상대운동이 있을 때에만 전류가 흐르고 상대 운동이 멈추면 전류도 사라진다.
운동이 빠를수록 더 큰 전류가 생긴다.
만일 자석의 N극을 전류고리 쪽으로 움직일 때 고리에 시계방향으로 전류가 흐른다면, N극이 고리에서 멀어질 때에는 반시계방향으로 전류가 흐른다. 자석의 S극을 고리에 접근시키거나 멀리할 때도 전류가 흐르지만 전류의 방향은 N극의 경우와는 반대이다.
전류고리에 생기는 전류는 유도전류라고 하고, 유도전류가 생기도록 단위전하당 한 일(전류는 전도전자들의 운동이다)을 유도기전력이라고 한다. 또한 전류와 기전력이 생기는 과정을 유도라고 한다.
두 번째 실험

이 실험에서는 위 그림처럼 서로 닿지 않은 채 가까이 있는 두 전류고리를 이용한다. 스위치 S를 당아 오른쪽 전류고리에 전류가 흐르게 되면 왼쪽 전류고리에 연결된 전류계에 유도전류가 순간적으로 생긴다. 다음에 스위치 S를 열어 전류가 흐르지 않게 되면 왼쪽 전류고리에 또다시 유도전류가 잠깐 생기지만 방향은 반대이다. 유도전류 혹은 유도기전력은 오른쪽 전류고리에 흐르는 전류가 변할 때에만(스위치를 닫거나 열 때) 생기고, 전류가 일정하면 그 양이 아무리 크더라도 유도전류가 생기지 않는다.
위의 두 실험에서 유도전류와 유도기전력은 어떤 변화가 일어날때만 생기는 것이 분명하다. 결국 이 변화의 정체를 Faraday가 알아냈다.
위 두 그림의 왼쪽 전류고리를 통과하는 자기장선의 수가 변할 때 전류 고리에 기전력이 유도된다. + 전류고리에 유도되는 기전력의 크기는 전류고리를 통과하는 자기다발의 시간변화율과 같다.

다시 정리하면

(4) Ampere-Maxwell의 법칙
앞의 페러데이 법칙을 보자. 유도현상이 반대 방향으로 일어날 수 있는가라는 질문이 생길 것이다. 즉, 전기다발의 변화가 자기장을 유도할 수 있을까?
그럴 수 있다. 자기장의 유도를 나타내는 식은 페러데이의 법칙과 거의 대칭적이다.

Ampere의 법칙에도 같은 적분 형태가 나타난다.

여기서 i는 닫힌 고리로 둘러싸인 전류이다. 따라서 자기물질이 아닌 다른 수단, 즉 전류나 변화하는 전기장으로 만들어지는 자기장을 나타내는 식이 정확히 같은 형태를 같는다. 두 식을 다음과 같이 하나의 식으로 결합할 수 있다.
